已知函数f(x)=asin(ωx+φ)(a>0,w>0)

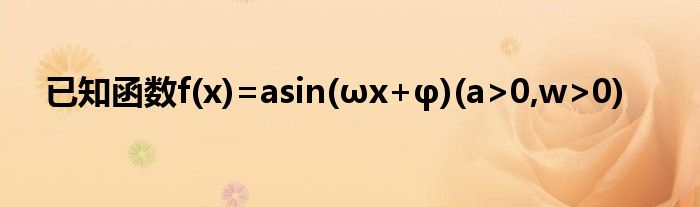
大家好,小讯来为大家解答以上的问题。已知函数f(x)=asin(ωx+φ)(a>0,w>0)这个很多人还不知道,现在让我们一起来看看吧！

1、根据题意：f(1+x)=f(1-x)，所以函数关于x=1对称函数是奇函数，故f(x-1)=-f(1-x)，所以：f(x+1)=-f(x-1)，所以函数是周期函数例如：解：∵f（x）是定义域为R的奇函数∴f（0）=0，且f（-x）=-f（x）∴f（1-x）=-f（x-1）又∵f（1+x）=f（1-x）∴f（1+x）=-f（x-1）∴f（x+2）=-f（x）且f（x+4）=-f（x+2）∴f（x+4）=f（x）∴原函数的周期为T=4∴f（2010）=f（2） f（2011）=f（-1）∵f（1+x）=f（1-x），且f（0）=0性质两个奇函数相加所得的和或相减所得的差为奇函数。

2、2、一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。

3、3、两个奇函数相乘所得的积或相除所得的商为偶函数。

4、4、一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。

5、以上内容参考：百度百科-奇函数数学之美团为你解答 根据题意：f(1+x)=f(1-x)，所以函数关于x=1对称又函数是奇函数，故f(x-1)=-f(1-x)，所以：f(x+1)=-f(x-1)，所以函数是周期函数且最小正周期是2|1+1|=4。

6、 x∈(0,1]时，f(x)=x，因f(x)是奇函数，所以在x∈[-1,0)，f(x)=x根据f(x)是R上的奇函数，知道函数在原点有定义，又函数关于x=1对称所以在区间[1,3]，f(x)=-x+2，又函数是周期为4的函数故在区间[3,5]，因：f(x)=f(x-4)=x-4 所以所求函数为：f(x)=-x+2，x∈[1,3]；f(x)=x-4，x∈[3,5]不好意思，我才看到求助，估计这问题你也解决了。

7、我下次再帮你f（x）=-x+2, x∈[1，3]；f（x）=x-4, x∈[3，5]；。

本文到此分享完毕，希望对大家有所帮助。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！